What are Trees?

Trees are data structures that consist of nodes that are connected by edges.

Nodes can represent real world entities such as people, houses, cities etc. Edges represent the relationship between the nodes.

Typically there is a single node at the top row of the tree, more on the second row, and gradually increasing as we go down the rows of the tree.

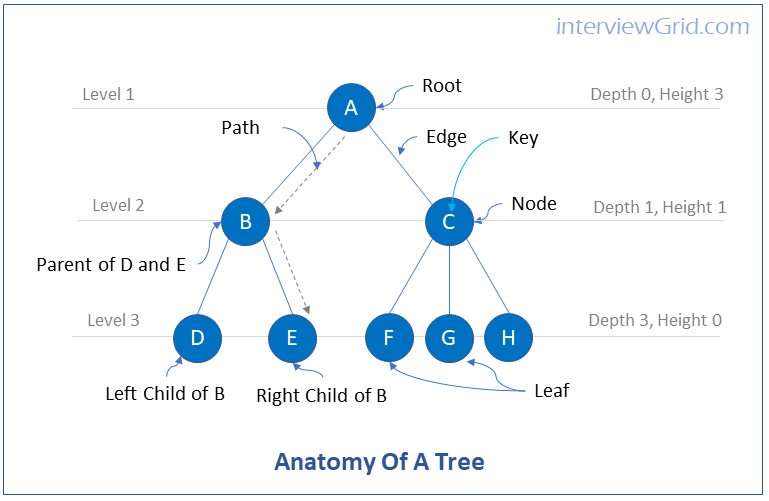
Tree Terminology

Root - Root is the top node of a tree. A tree can have only one root. Every node must have only one path to the root of the tree.

Edge - Edge is the line connecting from one node to another

Path - Path is the connection from one node to another along the edges, and spanning multiple nodes.

Parent - Every node has an edge going upwards and connecting to another node called as its parent node.

Child - Every node can have one or more edges going downwards and connecting to nodes called child nodes.

Leaf - a node that does not have child nodes is called a leaf node.

Key - The data value represented by a node is called the key.

Tree Representation

Nodes in a tree are represented by circles containing the key value. Edges are represented as lines between the circles.

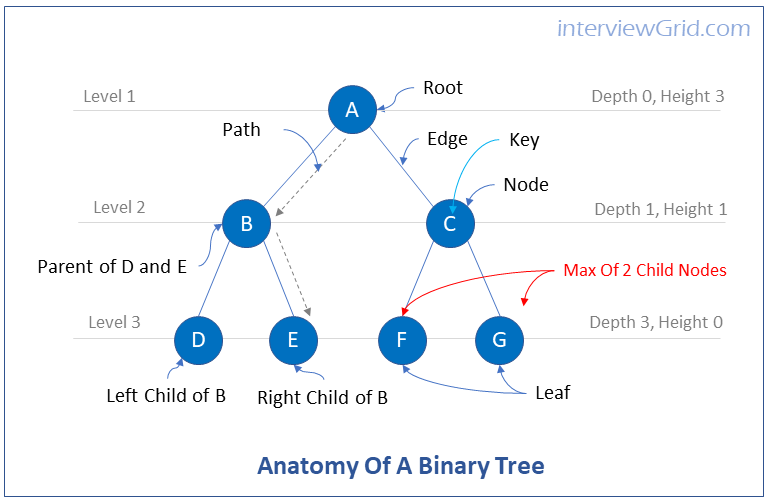
What are binary trees?

Binary trees are trees in which each node has at most two child nodes. The child node on the left is called the left child node and the child node on the right is called the right child node.

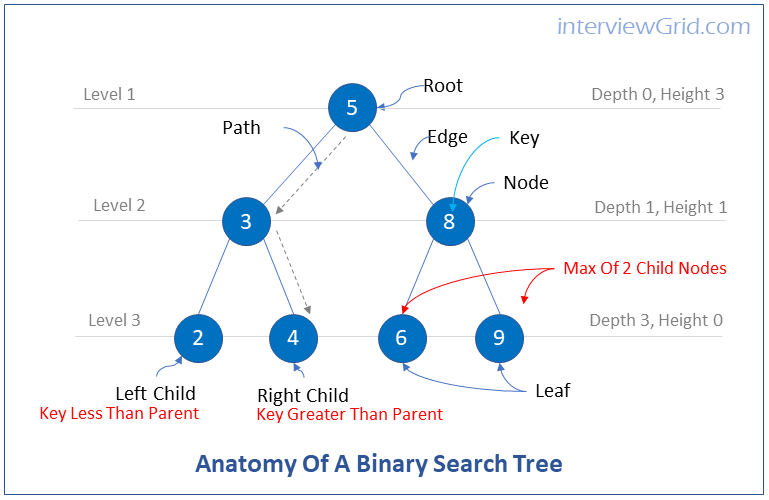
What are binary search trees?

Binary search trees are binary trees in which a parent node's left child must have a key less than the parent node, and a parent node's right child must have a key greater than the parent node.

Advantages of Binary Search Trees

Binary search trees have the advantages of both ordered arrays and linked lists.

Searches are quick with ordered arrays, but insertions and deletions are slow. Insertions and deletions are quick with linked lists, but searches are slow.

Searches, insertions and deletions are fast with binary search trees.

What is the difference between balanced vs Unbalanced binary tree?

In balanced trees there are approximately equal number of left descendant nodes and right descendant nodes. In unbalanced trees there are many more left descendant nodes than right descendant nodes, or vice versa.

What are the key operations performed on binary tree? What is their time efficiency

Insertions, Deletions, Searches are the common operations performed on binary search trees.

The time efficiency of these operation on binary search trees is O(logN)

Write code to represent the node in a binary search tree.

The node in a binary search tree has 4 key elements.
1. Key
2. Data
3. Reference to left child node
4. Reference to right child node

//Node
public class Node {
  public int key;
  public int data;
  public Node leftChild;
  public Node rightChild;
  //constructor
  public Node(int key, int data) {
    this.key = key;
    this.data = data;
    this.firstChild = null;
    this.rightChild = null;
  }
}

What are the key operations performed on binary tree? What is their time efficiency

Insertions, Deletions, Searches are the common operations performed on binary search trees.

The time efficiency of these operation on binary search trees is O(logN)

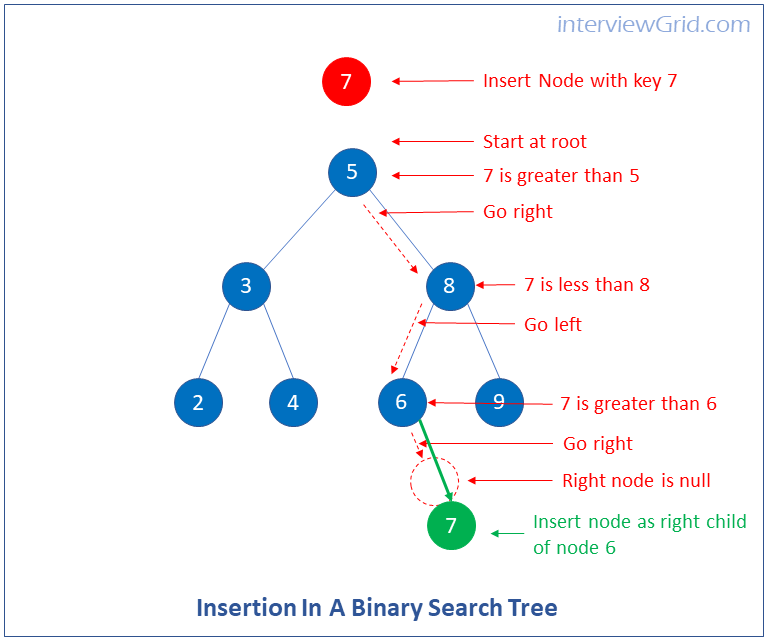
How do you insert a node in a binary search trees? Write a function to insert a node in a binary search tree.

You can insert a new node in a binary tree by traversing the binary tree and finding the position to insert the node, i.e. finding the parent node for the new node to be inserted. You can then insert the new node by making it a child node of the parent node.

Pseudocode
1. Start with the root (current node). If root is null then root = new node.
2. If key of new node is less than key of root then go to left node, else go to right node. this becomes the current node
3. If key of new node is less than current node then go to left child, else go to right child.
4. Repeat step 3 until current node is null.
5. If current node is left of parent node insert the new node here by referring the left child of parent node to new node.
6. If current node is right of parent node, insert the node here by referring the right child of the parent node to the new node.

How do you perform searches on binary search trees? Write a function to find a node in a binary search trees.

Following are key steps to perform searches on binary search trees.

1. Start at the root node and compare its value to the search key value.
2. If the search key value is less than the node value then go to the node's left child.
3. If the search key value is greater than the node value then go to the node's right child.

4. Repeat above steps for every child node that is visited.

How do you perform deletions on binary search trees? Write a function to delete from binary search trees.

Following are the key steps to perform insertions on binary search trees.

Perform search operation on the binary tree until the node to be deleted is found. The next steps depends on the number of child nodes that this node has. There are three possibilities

1. Node to be deleted has no children - If the node to be deleted has no children, i.e it is a leaf node, then just set the corresponding child reference (left child or right child) in the parent node to null.

2. Node to be deleted has one child - If the node to be deleted has only one child (say Node A), then set the corresponding child reference (left child or right child) in the parent node to this child node (Node A)

3. Node to be deleted has two children - If the node to be deleted has two children then replace the node with its in-order successor. The in-order successor is either the right child of the node to be deleted, or it can be a left descendant to right child of the node to be deleted.
A: In-order successor is the right child of the node to be deleted.
- Set the right child field (or left child field) of the parent node to the successor node.
- Set the left child field of the parent node to the left child field of the node to be deleted.
B: In-order successor is a left descendant to the right child of the node to be deleted
- successorParent.leftChild = successor.rightChild
- successor.rightChild = delNode.rightChild
parent.rightChild = successor
- successor.leftChild = current.leftChild