What are arrays?

Arrays are data storage structures that store data of same type (e.g. char, int, string etc.). Data values stored in the array are commonly referred to as elements of the array.

Structure of Arrays - Arrays are index based, i.e. every element stored in an array has an assigned index number and can be accessed using it's index number. The index of the first element of the array is 0, and the index of the last element of the array is (N-1) where N is the number of elements of the array. N is also referred to as the size of the array.

Arrays are fixed in size, i.e. once you declare an array of a specific length, it's size cannot be changed.

Memory
Memory allocated to an array depends on the size of array and the type of elements. For example, when you create an array of size 10 containing elements of type int (4 bytes), a contiguous memory of 40 bytes (4*10) is allocated for the array.

The array can then be referenced through the address of it's first byte, and an element of the array can be accessed through it's index number.

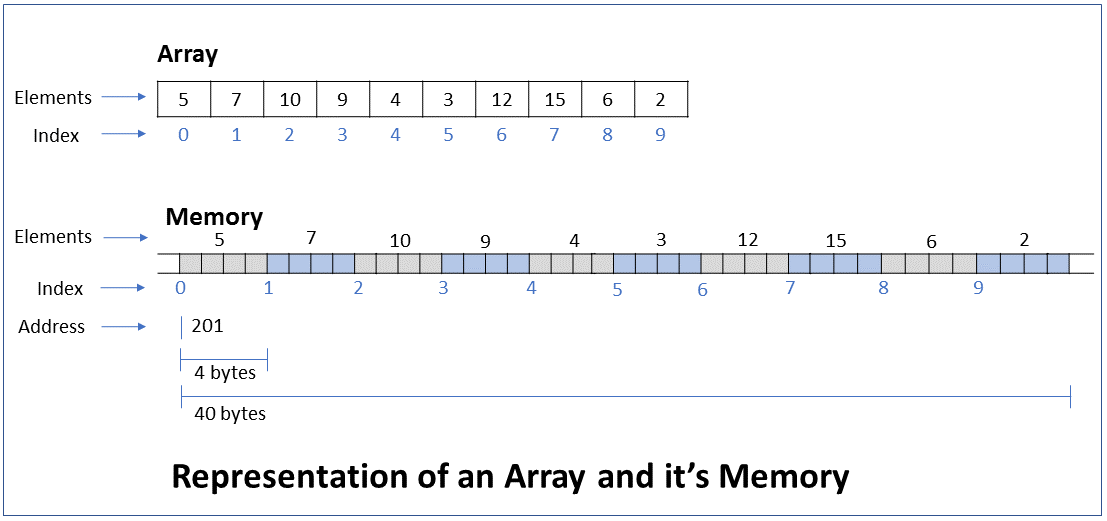
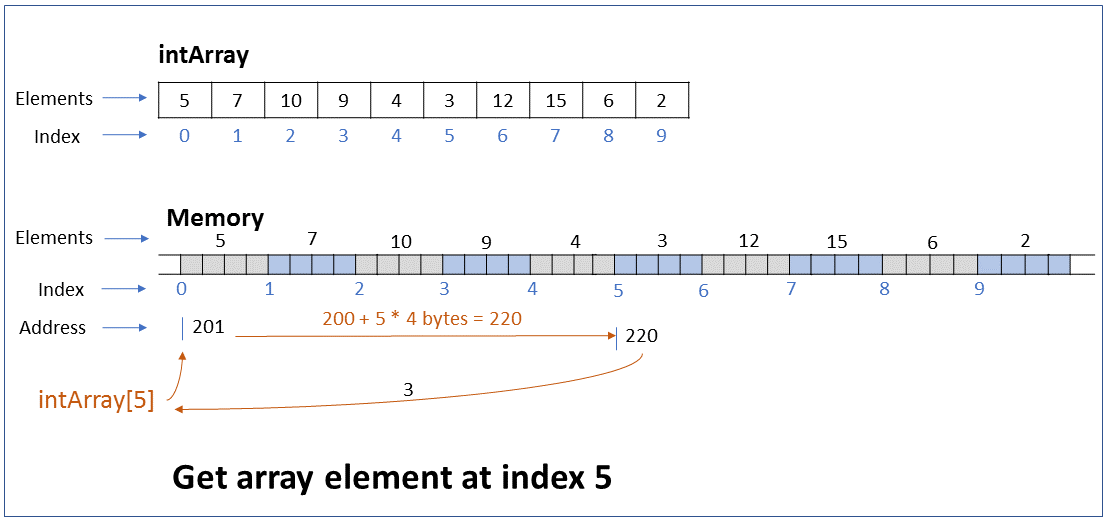
How do you read or update the value of an array element located at a particular index of the array? What is the efficiency of this operation?

The value of an array element can be read or updated by using the index number of the array.

The reference to an array refers to the address of the first byte of the array. When we request access to an element at a particular index, the computer calculates the address of this element based on the element type and index, and returns the element at that address.

For example, if the address of the first node of an int array is 201 and we request access to the element at index 5 (6th element), the computer returns the element at address 220 (200 + 5*4 bytes)

Performance - This operation executes a single step irrespective of the number of elements in the array, i.e. it takes constant time to run. In Big O notation the efficiency is O(1).

//Array of first 10 odd numbers
int[] intArray = {5, 7, 10, 9, 4, 3, 12, 15, 6, 2};

//print the value of array element at index 5
System.out.println(intArray[5]); //prints 3

//update the value of the array element at index 5 
intArray[5] = 21;
System.out.println(intArray[5]);//prints 21

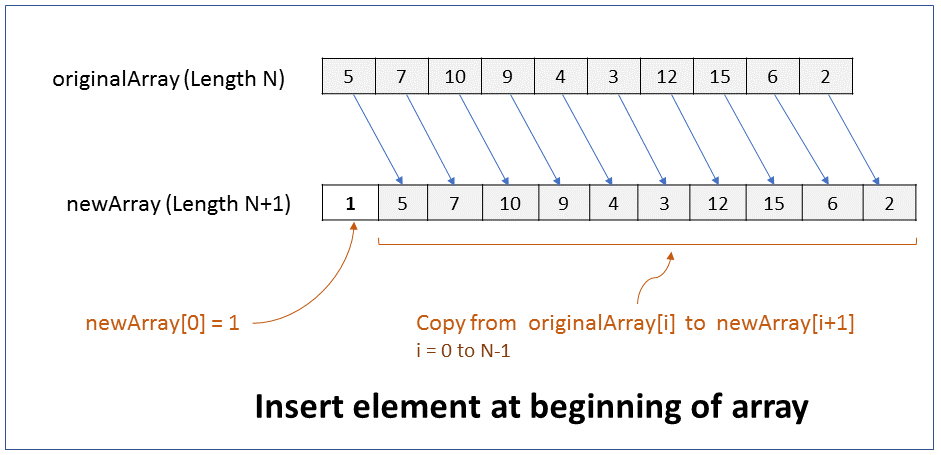
How do you insert an element at the beginning of an array? What is the efficiency of this operation?

The size of an array cannot be changed. Hence, to insert an element at the beginning of an array you have to create a new array of size 1 more than the original array, copy elements from original array to the new array, and then add the new element at index 0 of the new array.

Pseudocode
1. Create new array of size N+1, where N is size of original array.
2. Copy from originalArray[i] to newArray[i+1], where i = 0 to N-1
Add new element at newArray[0]

Performance - For an array of size N, it takes N steps to copy elements from original array to new array. It takes 1 step to add new element at index position 0. Therefore it takes linear time (N+1) to run. In Big O notation the efficiency of this operation is O(N).

//insert an element at the beginning of an array
public static int[] insertBeginning(int[] originalArray, int beginningValue) {
  //create new array with length 1 greater than the original array
  int[] newArray = new int[originalArray.length+1];
  //copy elements from original array to end of new array
  for(int i=originalArray.length-1; i>=0; i--) {
    newArray[i+1] = originalArray[i];
  }
  newArray[0] = beginningValue;
  return newArray;
}

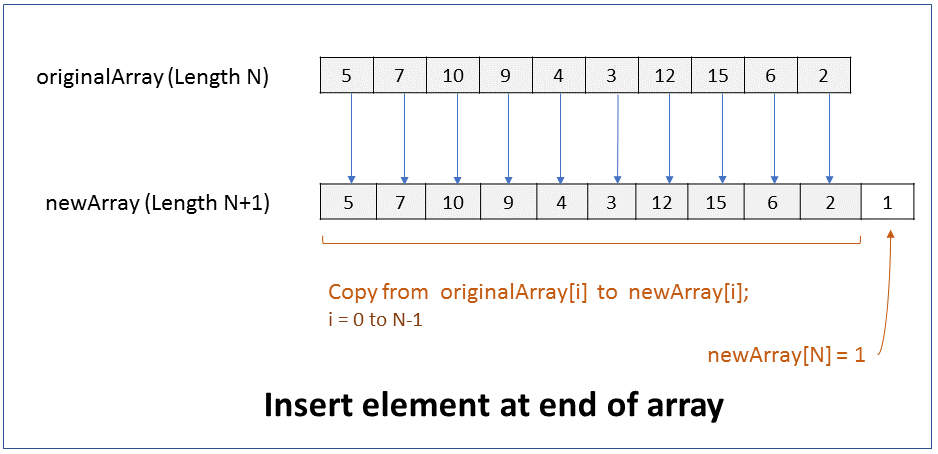
How do you insert an element at the end of an array? What is the efficiency of this operation?

The size of an array cannot be changed. Hence, to insert an element at the end of an array you have to create a new array of size 1 more than the original array, copy elements from original array to the new array, and then add the new element at last index of the new array.

Pseudocode
1. Create new array of size N+1, where N is size of original array.
2. Copy from originalArray[i] to newArray[i], where i = 0 to N-1
Add new element at newArray[N]

Performance - For an array of size N, it takes N steps to copy elements from original array to new array. It takes 1 step to add new element at last index position 0. Therefore it takes linear time (N+1) to run. In Big O notation the efficiency of this operation is O(N).

//insert an element at the end of an array
public static int[] insertEnd(int[] originalArray, int endValue) {
  //create new array with length 1 greater than original array
  int[] newArray = new int[originalArray.length+1];
  //copy values from original array to beginning of new array
  for(int i=0; i<originalArray.length; i++) {
    newArray[i] = originalArray[i];
  }
  newArray[originalArray.length] = endValue;
  return newArray;
}

How do you insert an element in the middle of an array? What is the efficiency of this operation?

The size of an array cannot be changed. Hence, to insert an element at any index K of an array you have to create a new array of size 1 more than the original array, copy elements from original array to the new array, and then add the new element at index k of the new array.

Pseudocode
1. Create new array of size N+1, where N is size of original array.
2. Copy from originalArray[i] to newArray[i], where i = 0 to k-1
3. Add new element at newArray[K]
4. Copy from originalArray[j-1] to newArray[j], where j = k+1 to N

Performance - For an array of size N, it takes N steps to copy elements from original array to new array. It takes 1 step to add new element at index position 0. i.e. it takes linear time to run. In Big O notation the efficiency is O(N).

//insert an element at the middle of an array
public static int[] insertMiddle(int[] originalArray, int index, int value) {
  //create a new array of length 1 greater than the original array
  int[] newArray = new int[originalArray.length+1];
  //Copy values from original array to new array 
  //from beginning until the insertion index position
  for(int i=0;i<index;i++) {
    newArray[i] = originalArray[i];
  }
  //insert value
  newArray[index] = value;
  //Copy values from original array to new array
  //from index+1 until the last position
  for(int i=index+1; i<=originalArray.length; i++) {
    newArray[i] =originalArray[i-1];
  }
  return newArray;
}

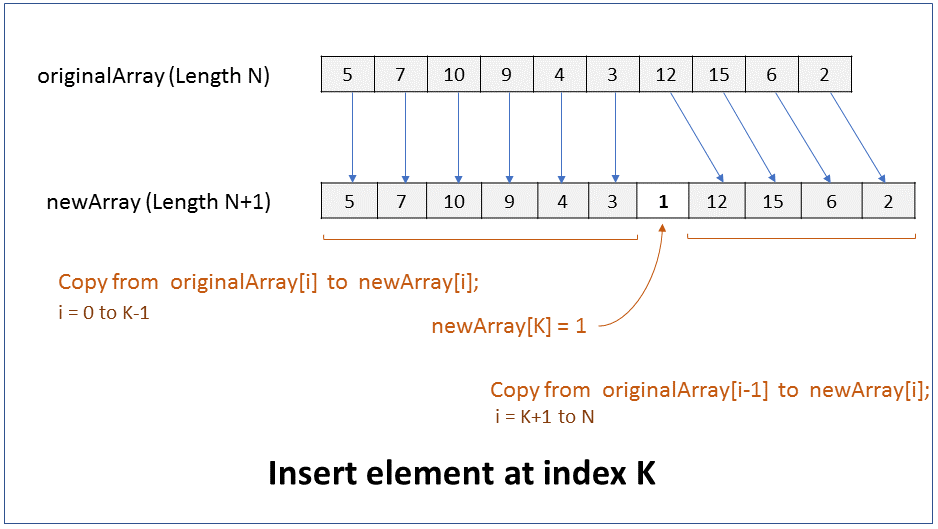
How do you delete an element from the beginning of an array? What is the efficiency of this operation?

We will assume that the size of the array must reduce by 1 after the element is deleted. i.e. there should not be a gap or hole in the array after the element is deleted.

The size of an array cannot be changed. Hence, to delete an element from the beginning of an array you have to create a new array of size 1 less than the original array, and copy all elements from original array to the new array except for the first element.

Pseudocode
1. Create new array of size N-1, where N is size of original array.
2. Copy from originalArray[i+1] to newArray[i], where i = 0 to N-1

Performance - For an array of size N, it takes N-1 steps to copy elements from original array to new array, ignoring the first element. Therefore it takes linear time (N-1) to run. In Big O notation the efficiency of this operation is O(N).

//delete an element from the beginning of an array
public static int[] deleteBeginning(int[] originalArray) {
  //Create new array of length 1 less that the original array
  int[] newArray = new int[originalArray.length-1];
  for(int i=0; i<originalArray.length-1; i++) {
    newArray[i] = originalArray[i+1];
  }
  return newArray;
}

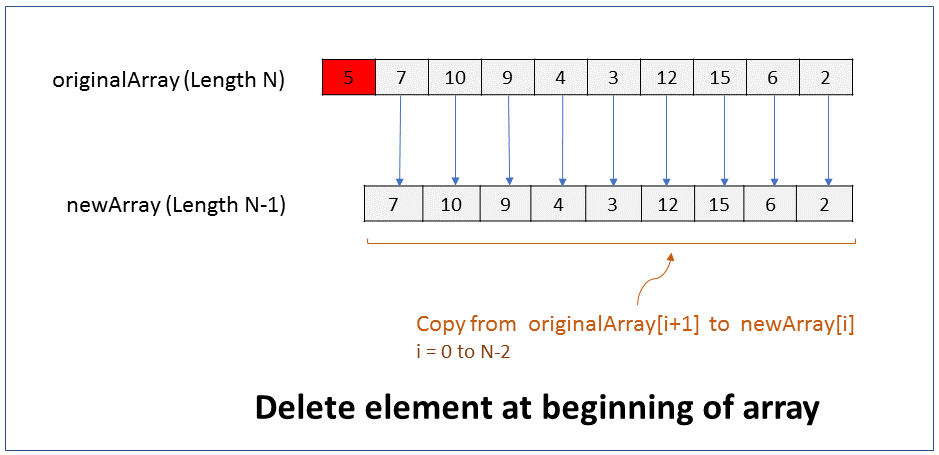
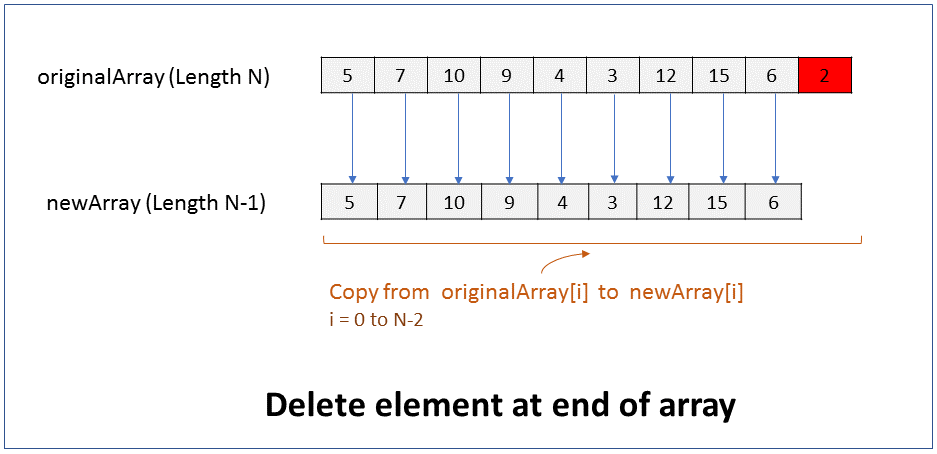
How do you delete an element from the end of an array? What is the efficiency of this operation?

We will assume that the size of the array must reduce by 1 after the element is deleted. i.e. there should not be a gap or hole in the array after the element is deleted.

Since the size of an array cannot be changed, to delete an element from the beginning of an array you have to create a new array of size 1 less than the original array, and copy all elements from original array to the new array except for the last element.

Pseudocode
1. Create new array of size N-1, where N is size of original array.
2. Copy from originalArray[i] to newArray[i], where i = 0 to N-2

Performance - For an array of size N, it takes N-1 steps to copy elements from original array to new array, ignoring the last element. Therefore it takes linear time (N-1) to run. In Big O notation the efficiency of this operation is O(N).

//delete an element from the end of an array
public static int[] deleteEnd(int[] originalArray) {
  //create new array of length 1 less than the original array
  int[] newArray = new int[originalArray.length-1]; //
  //copy values from old array to new array //
  for (int i=0; i<originalArray.length-1; i++ ) {
    newArray[i] = originalArray[i];
  }
  return originalArray;
}

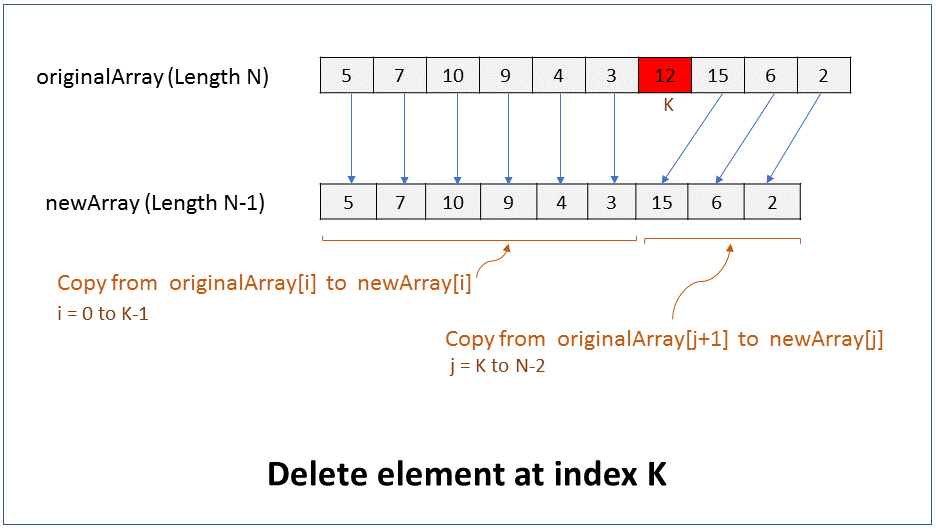
How do you delete an element in the middle of an array? What is the efficiency of this operation?

We will assume that the size of the array must reduce by 1 after the element is deleted. i.e. there should not be a gap or hole in the array after the element is deleted.

Since the size of an array cannot be changed, to delete an element from the beginning of an array you have to create a new array of size 1 less than the original array, and copy all elements from original array to the new array except for the element that has to be deleted.

Pseudocode
1. Create new array of size N-1, where N is size of original array.
2. Copy from originalArray[i] to newArray[i], where i = 0 to k-1
3. Copy from originalArray[j-1] to newArray[j], where j = k+1 to N

Performance - For an array of size N, it takes N-1 steps to copy all elements from original array to new array except for the element to be deleted. In Big O notation the efficiency is O(N).

//delete an element from the middle of an array
public static int[] deleteElement(int[] originalArray, int index) {
  //create new array of length 1 less than the original array
  int[] newArray = new int[originalArray.length-1];
  //loop through the array and copy elements from old array to new array until index
  for (int i=0; i<index; i++) {
    newArray[i] = originalArray[i];
  }
  //shift elements to left after index K
  for (int j=index;j<originalArray.length-1; j++)  {
    newArray[j] = originalArray[j+1];
  }
  return newArray;
}

How do you search an element from an array? What is the efficiency of this operation?

There are two kinds of searches that can be performed on arrays - Linear search and Binary search. Binary search is more efficient than linear search, but it can be performed only on sorted arrays.

Linear search - For unsorted arrays you can use linear search to find an element.

In linear search you loop through the array and compare the value of each element against the search value.

Performance - For an array of size N, it takes an average of N/2 steps to complete the operation. In the best case scenario if the match is found in the first element then only 1 step is used. In the worst case scenario if the elements exists at the end of the array, or if the element does not exist, then it takes N steps to perform the search operation.

The time efficiency of this operation in Big-O notation is O(N).

Binary search - For sorted arrays you can use binary search to search for an element.

In binary search you compare the search value with the value of the middle element of the array.
- If the search value is smaller then you compare the search value with the middle element of the first half of the array.
- If the search value is larger then you compare the search value with the middle element of the second half of the array.
- You continue this process until the element is found.

Performance - It takes log(N) steps to complete this operation. The time efficiency of this operation in Big-O notation is O(log N).

Write a function to search an array using linear search.

In a linear search you loop through the array element by element until the search value is found. In this function we assume that either duplicates are not allowed or you stop the search once the search value is found. Below is the code snippet for linear search.

The time complexity of this search is O(N).

public int findIndex(int searchKey, int[] intArray) {
 int foundIndex=-1;
 for(int i=0; i<intArray.length; i++) {
  if(intArray[i]==searchKey) {
    foundIndex = i;
    break;
  } 
 }
 return foundIndex;
}

Write a function to search an array using binary search.

In a binary search you compare the search value with the value of the middle element of the array.
- If the search value is smaller then you compare the search value with the middle element of the first half of the array. If the search value is larger then you compare the search value with the middle element of the second half of the array. You continue this process until the element is found. Below is the code snippet for binary search

The time complexity of this search is O(log N).

public int findIndex(int searchKey, int[] intArray) {
 int lowerBound = 0;
 int upperBound = intArray.length - 1;
 int currentIndex;
 while(true) {
  currentIndex = (lowerBound + upperBound)/2
  if(intArray[currentIndex]==searchKey) {
    return currentIndex;
  } else if(lowerBound > upperBound){
    //value not found
    return -1;
  } else if(intArray[currentIndex] < searchKey){
    //value in upper half
    lowerBound = currentIndex + 1;
  } else if(intArray[currentIndex] > searchKey){
    //value in lower half
    upperBound = currentIndex - 1;
  }
 }
}

How do you sort the elements in an array?

Sorting of data is an important concept in computer science. It is a preliminary step for many algorithms. For example - binary search which is much faster than linear search, requires data to be sorted before the binary search algorithm can be applied to data.

Extensive research and work has gone into this subject in computer science, resulting in improved and efficient sort algorithms along the years.

Following are the common sort algorithms that you have to know for your interview. Following questions address each of these sort algorithms.

1. Bubble Sort
2. Selection Sort
3. Insertion Sort
4. Shellsort
5. Quicksort
6. Radixsort

How do you sort the elements in an array using Bubble Sort algorithm?

Bubble sort is the simplest of sort algorithms but is also the slowest. It is a good algorithm to begin learning sorting techniques.

Approach
1. Start from the left of the array, i.e. index position 0.
2. Compare with the value at the next position, i.e. index 1. If the value at index 0 is greater than the value at index 1, then swap them.
3. Repeat step 2 for all adjacent pairs of values until the end of array is reached. At this point the last index of the array contains the highest value.
4. Repeat steps 1, 2, 3 until the whole array is sorted.

Performance - The time efficiency of Bubble sort operation in Big-O notation is O(N*2).

How do you sort the elements in an array using Selection Sort algorithm?

Selection Sort improves on the Bubble Sort by reducing the number of swaps from O(N*2) to O(N). The number of comparisons remain O(N).

Approach
1. Start from the left of the array, i.e. index position 0, and pass through all elements and select the smallest number. Swap the smallest number with number at position 0.

2. Start from the next position of the array, i.e. index position 1, and pass through all subsequent elements and select the smallest number. Swap the smallest number with number at position 1.

Repeat for all remaining elements, i.e. elements at index positions 2,3,4... until the last element of the array.

Performance - The time efficiency of Selection sort operation in Big-O notation is O(N*2).

How do you sort the elements in an array of numbers using Insertion Sort algorithm?

Insertion Sort works by marking an element as a marker element and partially sorting all numbers to the left of this marker element. We then insert the marker element and each element to the right of the marker element at the appropriate position in the partially sorted array.

Approach
1. Start by selecting one of the elements, usually an element in the middle of the array, as a marker element.

2. Sort all the elements to the left of the marker element.

3. Insert the marker element at appropriate position in the sorted array such that the sort order is maintained. Shift all elements with a value greater than the marker element one position to the right to make way for the marker element.

4. Repeat step 3 for each of the elements to the right of the marker element.

Performance - - The time efficiency of Insertion sort operation in Big-O notation is O(N*2).

How do you sort the elements in an array of numbers using Quick Sort algorithm?

Quicksort is the fastest in-memory sort algorithm in most situations. Quicksort algorithm works by partitioning an array into two subarrays, and the recursively calling itself to sort the subarrays.

Approach
1. Partition the array into left and right subarrays.
2. Call recursively to sort the left subarray
3. Call recursively to sort the right subarray.

Performance - - The time efficiency of Insertion sort operation in Big-O notation is O(N*logN).

Find largest number in an array of integers.

Given an array of integers, find the largest number in the array.

See Solution >>

Find smallest and largest number in an array of integers.

Given an array of integers, find the smallest and the largest number in the array.

See Solution >>

Find the running sum of an array of integers.

Given an array of integers, return a new array containing the running sum of integers of first array.

See Solution >>

Find count of numbers that are smaller than the current number.

Given an array of integers, return a new array containing the count of numbers that are less than the current number.

See Solution >>

Find the sum of digits of the smallest number in an array.

Given an array of integers, find the sum of digits of the smallest number in the array.

See Solution >>

Find the pivot index in an array of integers.

Given an array of integers, find the index (pivot index) where the left sum equals the right sum.

See Solution >>